Физобраз | Общее физическое образование

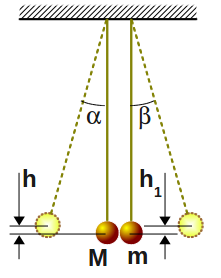Обозначим через l длину нитей, через M массу левого, а через m массу правого шара. В начальный момент левый шар находится на высоте h=l(1-cos α) от нижней точки. Из закона сохранения энергии следует, что скорость левого шара v в момент столкновения удовлетворяет условию:

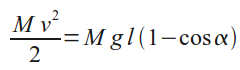
откуда

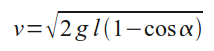
Так как второй шар после соударения поднялся на высоту h_1=l(1-cos β), то он имел скорость

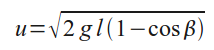
Но при столкновении шаров их суммарный импульс не изменился, поэтому

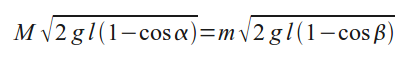
Откуда

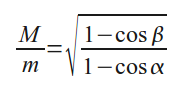
Обозначим через W механическую энергию, теряемую при первом столкновении. Тогда

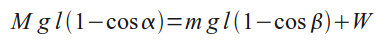
Пусть отношение энергии W к максимальной потенциальной энергии W_p деформации шаров равно k. Так как в момент максимальной их деформации шары движутся как одно целое со скоростью v_0, то

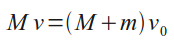
откуда

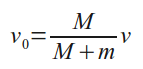
Из закона сохренения энергии следует, что

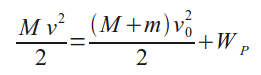
откуда

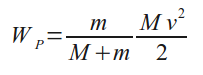
Так как

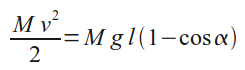
то

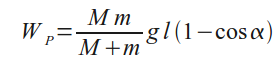
или

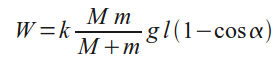
Подставим это выражение в формулу для потерь и получим

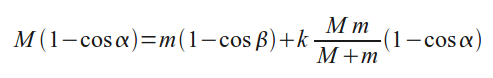
Обозначим через γ угол отклонения левого, а через δ угол отклонения правого шара после второго столкновения. Рассуждая так же, как и для первого столкновения, получим

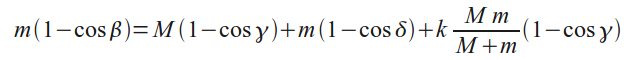
С другой стороны, из условия сохранения импульса при втором столкновении имеем

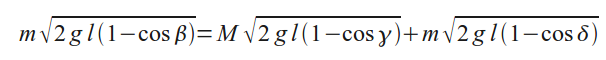
Из двух последних уравнений (учтя соотношение масс шаров) получаем: