Физобраз | Общее физическое образование

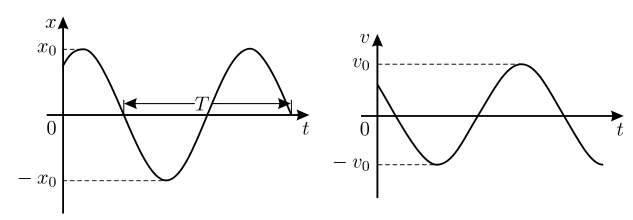
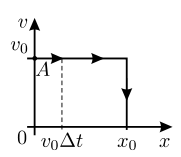а) Пусть в начальный момент времени координата материальной точки равна 0, а её скорость v = v_0 (точка A на зависимости v(x), см. рис.). Тогда через маленький промежуток времени ∆t координата x материальной точки станет равной v_0 ∆t > 0. Это соответствует тому, что точка на нашем графике v(x) будет смещаться вправо. Так будет продолжаться до момента времени ∆t_1 = x_0 /v_0, после которого знак скорости изменится: вместо v = v_0 станет v = −v_0. Таким образом, в течение времени ∆t_1 материальная точка будет двигаться с постоянной скоростью v_0.
Затем в течение времени ∆t_2 = 2x_0 /v_0 материальная точка будет двигаться с постоянной скоростью −v_0, после чего знак скорости вновь изменится — она станет равной v_0. Далее материальная точка будет двигаться с этой скоростью в течение времени ∆t_3 = x_0 /v_0, после чего вернётся в исходное положение, и цикл движения повторится. График зависимости скорости от времени v(t), соответствующий описанному движению, приведён на рисунке.
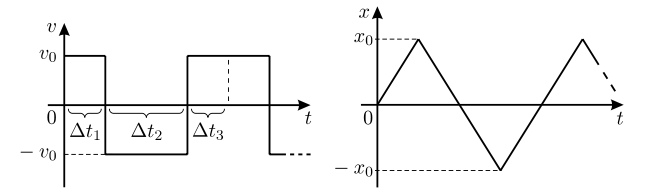По полученному графику v(t) легко построить график зависимости координаты от времени x(t). Действительно, «ступеньки» графика v(t) соответствуют движениям с постоянными скоростями v_0 или −v_0.
При движении с постоянной скоростью зависимость координаты от времени даётся формулой x = x(0) + vt. В начале движения x(0) = 0, и x = v_0 t. Через время ∆t_1 координата материальной точки станет равной x_0, а скорость примет значение −v_0, то есть зависимость x(t) будет даваться формулой x = 2x_0 − v_0 t. Такая зависимость будет справедлива в течение промежутка времени ∆t_2, после чего координата станет равна −x_0, а скорость примет значение v_0. В результате зависимость x(t) приобретёт вид x = −4x_0 + v_0 t. График зависимости x(t) приведён на рисунке. Это периодическое движение с периодом

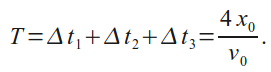
В заключение остановимся на вопросе о практической реализации такого движения. Понятно, что в реальности оно существовать не может, так как мгновенная смена знака скорости при x = x_0 и x = −x_0 означает, что в данные моменты времени материальная точка имеет бесконечно большое ускорение. Однако, можно представить себе движение, близкое к тому, о котором идёт речь в условии. Это может быть, например, движение маленького шарика, который в отсутствие сил тяжести и трения летает по прямой между двумя параллельными стенками, испытывая с ними абсолютно упругие соударения.

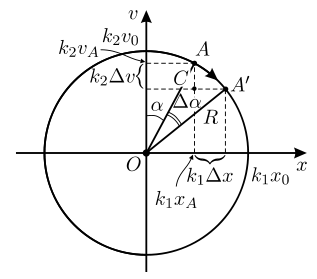б) Обозначим на графике v(x) начало координат точкой O (см. рис.), а радиус окружности через R. Тогда, очевидно, можно записать:
R = k_1 x_0 = k_2 v_0,
где k_1 и k_2 — положительные размерные масштабные коэффициенты.
Пусть в некоторый момент времени скорость и координата материальной точки таковы, что они соответствуют на графике v(x) точке A с координатами (k_1 x_A , k_2 v_A ). Обозначим угол, который составляет радиус OA с осью Ov, через α. Так как в рассматриваемый момент времени скорость материальной точки положительна, то за малое время ∆t она сместится на положительное расстояние ∆x, что соответствует на графике точке A. Это означает, что радиус OA повернётся по часовой стрелке, и угол, который он составляет с осью Ov, изменится на величину ∆α. При этом координаты точки A изменятся на величины k_1 ∆x и k_2 ∆v. Так как промежуток времени ∆t мал, то дугу окружности AA = R∆α можно приближённо заменить на хорду AA. Тогда из прямоугольного треугольника ACA получаем: k_1 ∆x ≈ R∆α cos α = k_1 x_0 ∆α cos α, откуда ∆x = x_0 ∆α cos α = v_A ∆t. Но, с другой стороны, как видно из чертежа, k_2 v_A = R cos α = k_2 v0 cos α, откуда v_A = v_0 cos α.
Подставляя v_A в выражение для ∆x, получаем

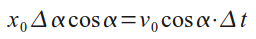
откуда

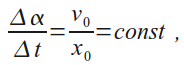
то есть радиус OA вращается с постоянной угловой скоростью ω = v_0 /x_0. Следовательно, угол α возрастает со временем по линейному закону: α = α_0 + ωt, где постоянная величина α_0 соответствует начальному положению точки A на окружности. С учётом этого получаем
k_1 x_A = R sin α = k_1 x_0 sin α,
откуда

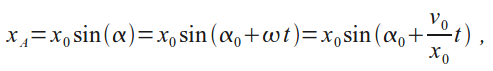
и аналогично

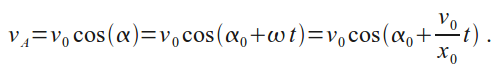
Из полученных зависимостей следует, что материальная точка совершает гармоническое колебание с амплитудой x_0 и периодом T = 2π/ω = 2πx_0 /v_0. Графики зависимостей x(t) и v(t), соответствующие данному движению, приведены на рисунке.