102032 - Шар в кольце
Так как заземляющий сферу проводник является тонким и длинным, то можно пренебречь электрическим полем этого проводника и считать, что кольцо со сферой настолько удалены от других тел, что их влиянием можно пренебречь. В силу сказанного и с учётом того, что сфера расположена симметрично относительно кольца, можно считать, что заряд Q распределён по кольцу равномерно.
Разобьём кольцо на малые элементы, каждый из которых можно считать точечным зарядом величины ΔQ. Как известно, поверхность нулевого потенциала поля, создаваемого двумя не равными по величине и противоположными по знаку точечными зарядами, имеет вид сферы, окружающей меньший по модулю заряд. Следовательно, поле, создаваемое точечным зарядом ΔQ, находящимся на расстоянии R от центра заземлённой сферы, и зарядами, имеющимися на заземлённой сфере радиуса r < R, вне сферы должно совпадать с полем точечных зарядов ΔQ и -Δq при определённых величине и расположении последнего. Из соображений симметрии следует, что заряд -Δq должен находиться на
прямой, соединяющей центр данной сферы и заряд ΔQ. Кроме того,очевидно, что заряд -Δq должен находиться внутри сферы. Если расстояние от заряда -Δq до центра сферы равно ρ, то, поскольку все точки сферы имеют нулевой потенциал, должны выполняться соотношения:
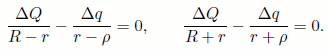
Отсюда:
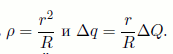
Приведённые рассуждения справедливы для любого элемента кольца. Из сказанного следует, что поле вне сферы в рассматриваемой задаче эквивалентно полю двух коаксиальных колец — радиуса ρ с зарядом Q и радиуса R с зарядом
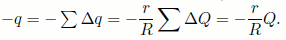
Поскольку потенциал поля кольца радиуса R с равномерно распределённым по нему общим зарядом Q на оси кольца на расстоянии x от его плоскости равен
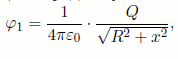
то искомый потенциал:
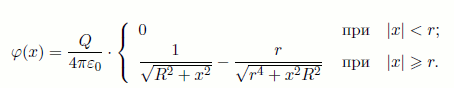
- Войдите на сайт для отправки комментариев
