Основы
Задача о перколяции
пн, 08/29/2011 - 17:15 — ofo_adminКласс: 10, 11, 8, 9
Задачи о перколяции — прекрасный пример использования моделирования для изучения критических явлений. С одной стороны, теоретически (и аналитически) изучать критические процессы в школе едва ли возможно. С другой стороны, моделирование их не требует никаких серьёзных познаний в физике, но позволяет получать довольно интересные результаты.
- Войдите на сайт для отправки комментариев
- Подробнее
Введение в хаос
птн, 08/26/2011 - 21:00 — ofo_adminКласс: 10, 11, 9
Физика в школе выглядит такой простой и логичной, а реальный мир наполнен самыми невероятными и необъяснимыми явлениями. Взять хотя бы погоду.
Каким образом у самых простых систем появляется очень сложное поведение? Попробуем исследовать этот процесс на примере нескольких моделей.
- Войдите на сайт для отправки комментариев
- Подробнее
Время реакции
вт, 08/23/2011 - 14:23 — ofo_adminКак измерить время реакции человека? Очень интересная задачка для семиклассников, только начавших изучать физику. Наглядно демонстрирует все сложности планирования хорошего эксперимента.
Класс: 6, 7
- Войдите на сайт для отправки комментариев
- Подробнее
Скорость дождевых капель
вс, 08/21/2011 - 00:08 — ofo_adminКак измерить скорость падения дождевых капель?
Когда смотришь на дождь из окна квартиры, иногда кажется, что капли летят так медленно!
Может, попробовать измерить их скорость?
Класс: 7, 8
- Войдите на сайт для отправки комментариев
- Подробнее
072016-Разорвать бечёвку
вт, 08/02/2011 - 13:50 — ofo_adminКласс: 7, 8, 9
Трудность: 2
Почему мокрую бумажную верёвку разорвать легче, чем сухую?
101004-Вселенские единицы
вс, 07/24/2011 - 19:02 — ofo_adminКласс: 10, 11
Трудность: 1
Ученые обратили внимание на то, что единицы длины, времени и массы «приспособлены» к людям и связаны с особенностями планеты Земля, но могут оказаться «неудобными» при контактах с представителями внеземных цивилизаций. Поэтому было предложено в качестве основных механических единиц взять фундаментальные постоянные c ≈ 3∙10^8 м/с, G ≈ 7∙10^−11 Н∙м^2/кг^2 и ħ ≈ 1∙10^−34 Дж∙с. Тогда единицы длины l_P, времени t_P и массы m_P будут производными от этих физических величин и выражаться через них. Такие единицы назвали планковскими.
072013-Вес букв
пн, 07/18/2011 - 18:44 — ofo_adminКласс: 7, 8
Трудность: 2
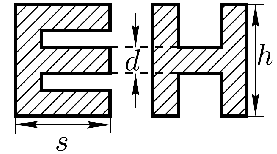Экспериментатор Глюк решил оформить стенд о своих научных достижениях. Чтобы сделать красивый заголовок стенда, он выпилил лобзиком буквы из однородного листа тонкой фанеры. Измерив массу некоторых из получившихся букв, Глюк с удивлением обнаружил, что буквы Е и Н имеют одну и ту же массу. У всех букв высота h = 8 см, ширина s = 5 см, а толщина линий d одинакова (рис. 4). Чему равна толщина d?
073005-Март и декабрь
чтв, 07/07/2011 - 18:11 — ofo_adminКласс: 7, 8
Трудность: 3
Почему в марте продолжительность дня меняется быстрее, чем в декабре?
082009-Коэффициент теплового расширения
пн, 06/27/2011 - 11:58 — ofo_adminКласс: 10, 8, 9
Трудность: 2
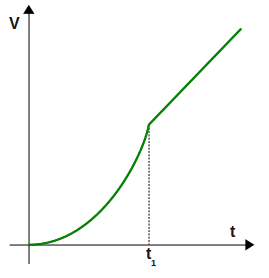График зависимости объёма тела от температуры в интервале от нуля до t1 представляетс собой параболу, переходящую при t1 в прямую, не являющуюся касательной к параболе.
Как зависит коэффициент теплового расширения этого тела от температуры до точки t1 и после?
Что можно сказать об этом коэффициенте в самой точке t1?
