10
092024-Прямоугольник и круг
сб, 09/17/2011 - 17:17 — ofo_adminКласс: 10, 9
Трудность: 2
 Материальная точка движется вдоль прямой. Постройте графики зависимостей скорости и координаты точки от времени, если график зависимости её скорости v от координаты x представляет собой:
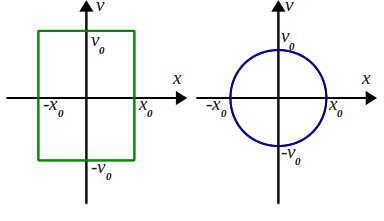
Материальная точка движется вдоль прямой. Постройте графики зависимостей скорости и координаты точки от времени, если график зависимости её скорости v от координаты x представляет собой:
а) прямоугольник;
б) окружность (при определённом выборе масштабов осей).
082021-Скорость пропорциональна расстоянию
сб, 09/17/2011 - 09:01 — ofo_adminКласс: 10, 8, 9
Трудность: 2
 Тело движется по прямой. График зависимости его скорости v от координаты x приведён на рисунке. Найдите ускорение тела в точке с координатой x = 3 м. Найдите также максимальное ускорение тела на отрезке от 0 до 5 м.
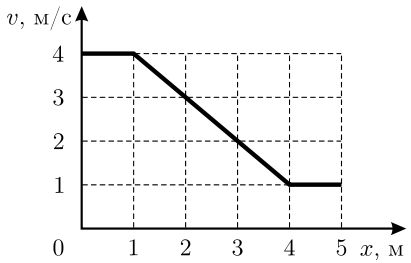
Тело движется по прямой. График зависимости его скорости v от координаты x приведён на рисунке. Найдите ускорение тела в точке с координатой x = 3 м. Найдите также максимальное ускорение тела на отрезке от 0 до 5 м.
082020-Пробка на светофоре
чтв, 09/15/2011 - 20:58 — ofo_adminКласс: 10, 8, 9
Трудность: 2
Мэр одного городка начал получать жалобы на большую автомобильную пробку перед светофором на главной улице. Скорость машин при движении составляла 6 м/c, а средняя скорость продвижения по пробке — всего 1,5 м/с. При этом время свечения светофора зелёным светом было равно времени свечения красным (время свечения жёлтым светом гораздо меньше). Мэр распорядился увеличить время свечения светофора зелёным светом в два раза, а время свечения красным светом оставить прежним. Чему станет равна средняя скорость продвижения машин по пробке?
092023-По двум конвейерам
пн, 09/12/2011 - 00:12 — ofo_adminКласс: 10, 7, 8, 9
Трудность: 2
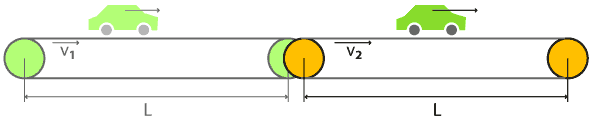
В автомобиле спидометр и счётчик пройденного пути регистрируют скорость автомобиля и пройденный им путь относительно поверхности, по которой движется автомобиль. Автомобиль последовательно проехал по двум конвейерам (движущимся дорожкам) длиной L = 500 м каждый. Полотна конвейеров движутся в одну сторону с постоянными скоростями v_1 = 20 км/ч и v_2 = 30 км/ч.
Молния
ср, 08/31/2011 - 10:07 — ofo_adminКласс: 10, 11, 9
Хотя молния и представляет собой обычный пробой диэлектрика, на любой фотографии она выглядит достаточно замысловато и живописно. Попробуем смоделировать сложный и хаотичный характер молнии.
- Войдите на сайт для отправки комментариев
- Подробнее
Задача о перколяции
пн, 08/29/2011 - 17:15 — ofo_adminКласс: 10, 11, 8, 9
Задачи о перколяции — прекрасный пример использования моделирования для изучения критических явлений. С одной стороны, теоретически (и аналитически) изучать критические процессы в школе едва ли возможно. С другой стороны, моделирование их не требует никаких серьёзных познаний в физике, но позволяет получать довольно интересные результаты.
- Войдите на сайт для отправки комментариев
- Подробнее
Случайные блуждания
вс, 08/28/2011 - 17:19 — ofo_adminКласс: 10
Хотя общая физика и не изучает пьяниц, но моделирование передвижения пьяницы около фонарного столба (случайного блуждания) оказывается очень полезным и интересным. Самым известным приложением таких моделей оказывается, например, изучение броуновского движения. Другими важными приложениями являются изучение диффузии и моделирование длинных полимерных цепочек.
- Войдите на сайт для отправки комментариев
- Подробнее
Силовые линии
сб, 08/27/2011 - 10:53 — ofo_adminКласс: 10, 8, 9
Линии напряжённости электрического и магнитного поля часто остаются "вещью в себе" для восьмиклассников. Да и в 10 классе не все ясно понимают, что это и зачем это. Может быть, если мы научимся их строить для самых разнообразных случаев, ореол загадочности улетучится сам собой?
- Войдите на сайт для отправки комментариев
- Подробнее
Введение в хаос
птн, 08/26/2011 - 21:00 — ofo_adminКласс: 10, 11, 9
Физика в школе выглядит такой простой и логичной, а реальный мир наполнен самыми невероятными и необъяснимыми явлениями. Взять хотя бы погоду.
Каким образом у самых простых систем появляется очень сложное поведение? Попробуем исследовать этот процесс на примере нескольких моделей.
- Войдите на сайт для отправки комментариев
- Подробнее
Движение спутников и планет
птн, 08/26/2011 - 18:16 — ofo_adminКласс: 10, 9
Сдувает ли спутники "солнечный ветер"?
Может ли маленький метеорит "сбить" Международную космическую станцию?
Вокруг чего, в конце концов, вращается Луна — вокруг Земли или вокруг Солнца?
И чем так страшна "задача трёх тел"?
- Войдите на сайт для отправки комментариев
- Подробнее
- « первая
- ‹ предыдущая
- …
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- …
- следующая ›
- последняя »
